Present Annuity Formula
The present value of annuity formula determines the value of a series of future periodic payments at a given time.
Present annuity formula. Pv c5 c6 c4 0 0 explanation an annuity is a series of equal cash flows spaced equally in time. An ordinary annuity pays interest at the end of a particular period rather than at the beginning. The present value of the coupon payments can be calculated as follows. The present value of annuity formula relies on the concept of time value of money in that one dollar present day is worth more than that same dollar at a future date.
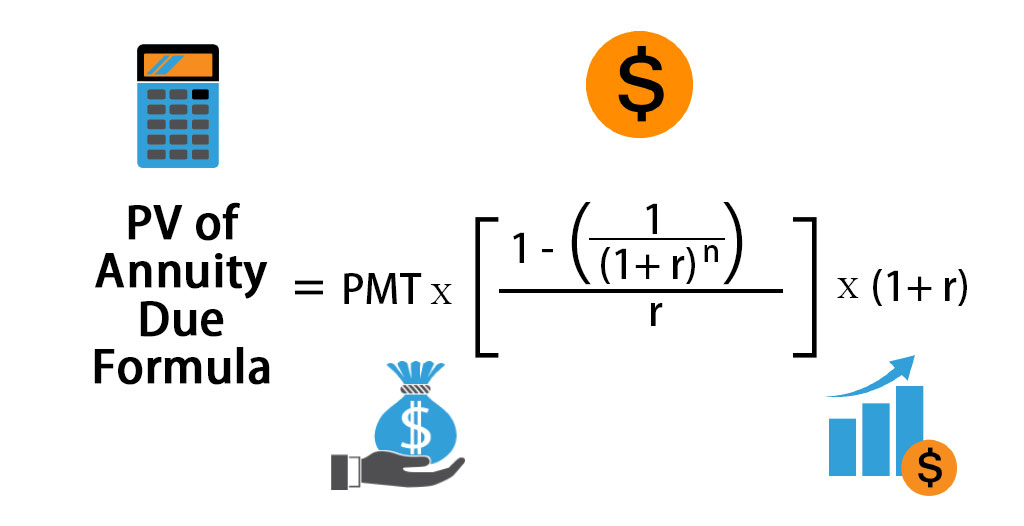
Using the present value formula above we can see that the annuity payments are worth about 400 000 today assuming an average interest rate of 6 percent. The formula for the present value of an annuity due identifies 3 variables. The annuity payment formula shown is for ordinary annuities. The formulas described above make it possible and relatively easy if you don t mind the math to determine the present or future value of either an ordinary annuity or an annuity due.
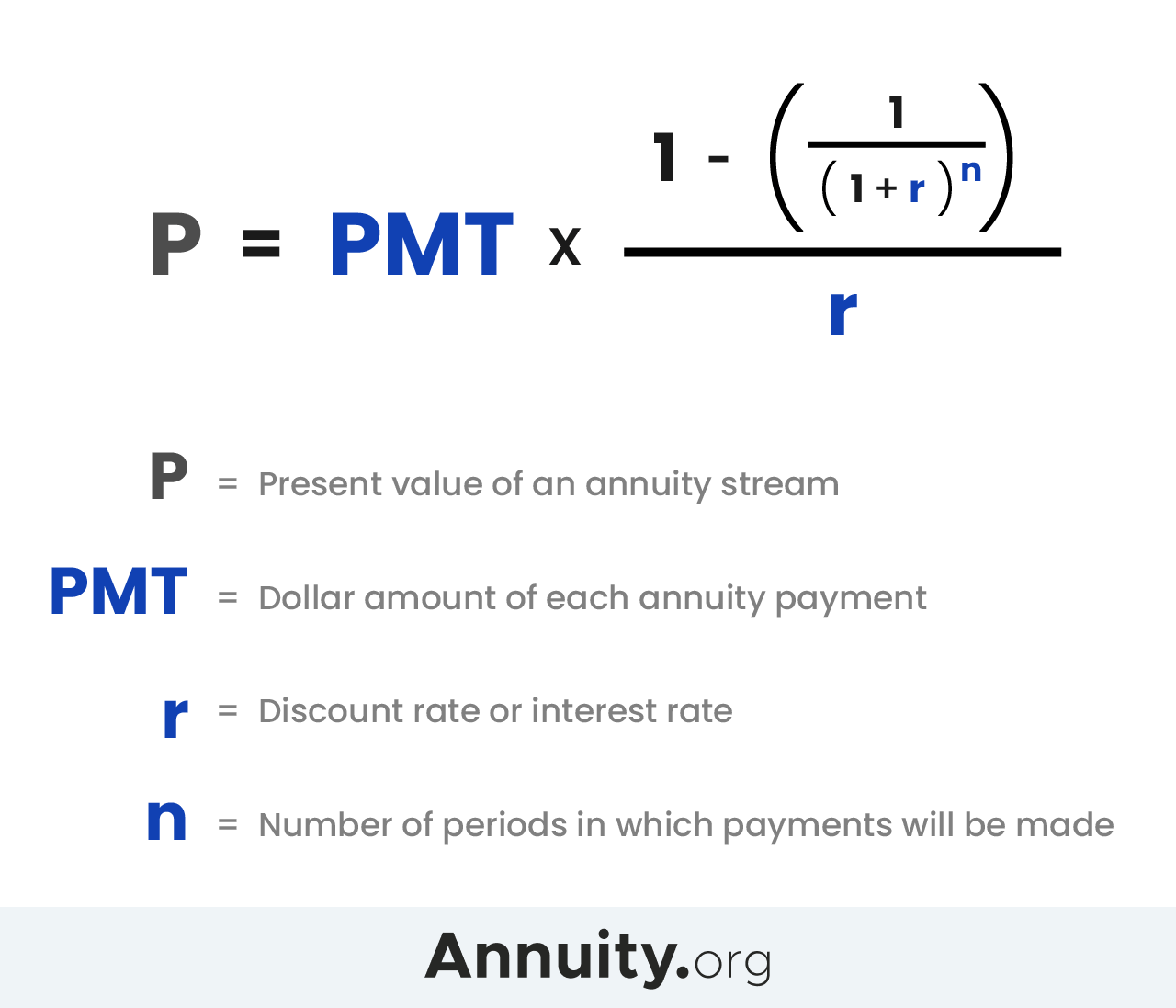
Present value of an annuity due calculator you can use the present value of an annuity due calculator below to work out the cash value of your immediate investment by entering the required numbers. The present value portion of the formula is the initial payout with an example being the original payout on an amortized loan. This formula assumes that the rate does not change the payments stay the same and that the first payment is one period away. Present value of ordinary annuity 1 000 1 1 5 4 6 4 5 4 present value of ordinary annuity 20 624 therefore the present value of the cash inflow to be received by david is 20 882 and 20 624 in case the payments are received at the start or at the end of each quarter respectively.
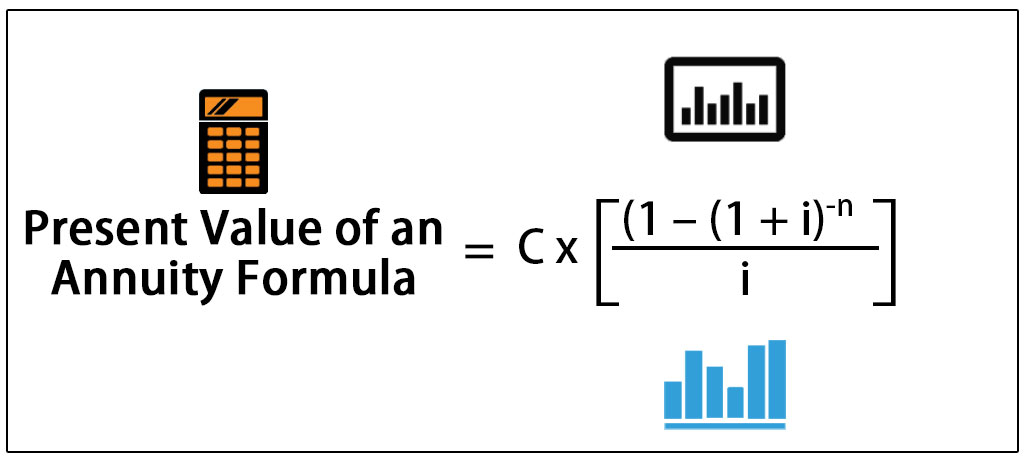
The present value of annuity formula is calculated by determining present value which is calculated by annuity payments over the time period divided by one plus discount rate and the present value of the annuity is determined by multiplying equated monthly payments by one minus present value divided by discounting rate. The formula for the present value of an ordinary annuity as opposed to an annuity due is below. Johnson is better off taking the lump sum amount today and investing in himself. The first four cash flows form an annuity and the final term is the present value of a single sum.
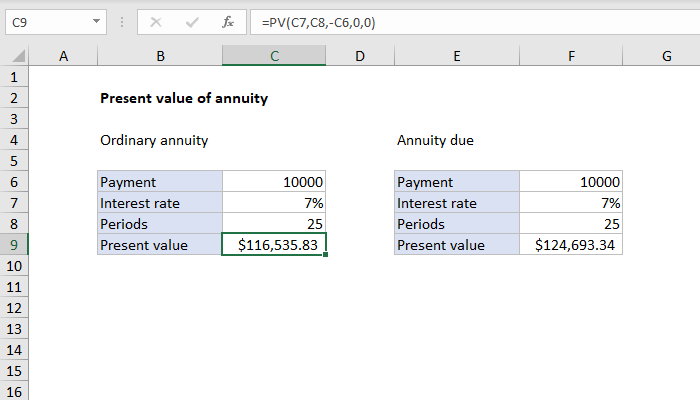
The cash value of payments the interest rate and the number of payments. Here if we change the discount rate then present value changes drastically. In the example shown the formula in c9 is.
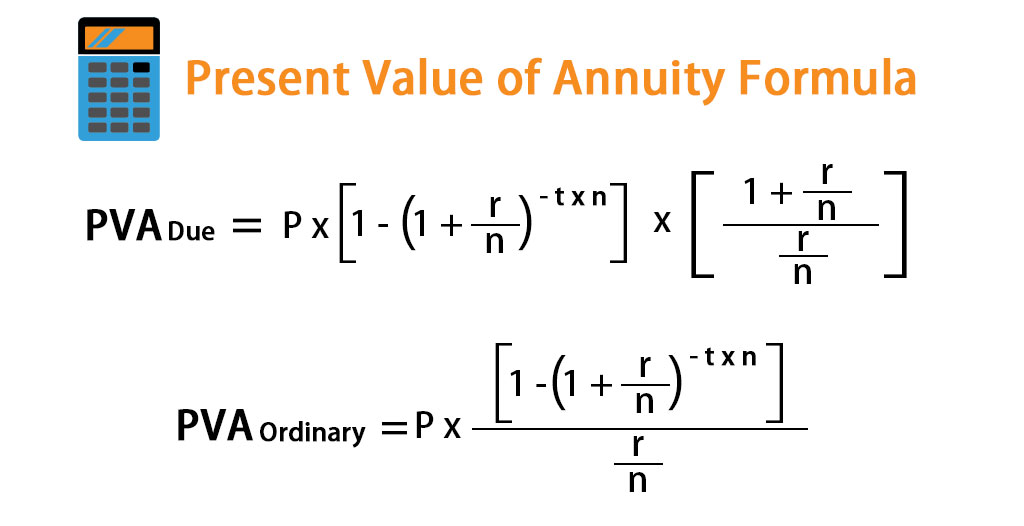

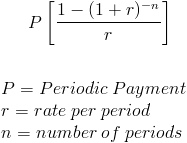
:max_bytes(150000):strip_icc()/CalculatingPresentandFutureValueofAnnuities3-f5e4d156c37b4fffb4f150266cea32b1.png)

:max_bytes(150000):strip_icc()/CalculatingPresentandFutureValueofAnnuities5-d76f3a6c09a54703afa365a16aff6607.png)





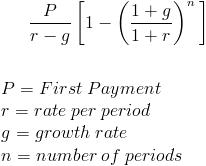
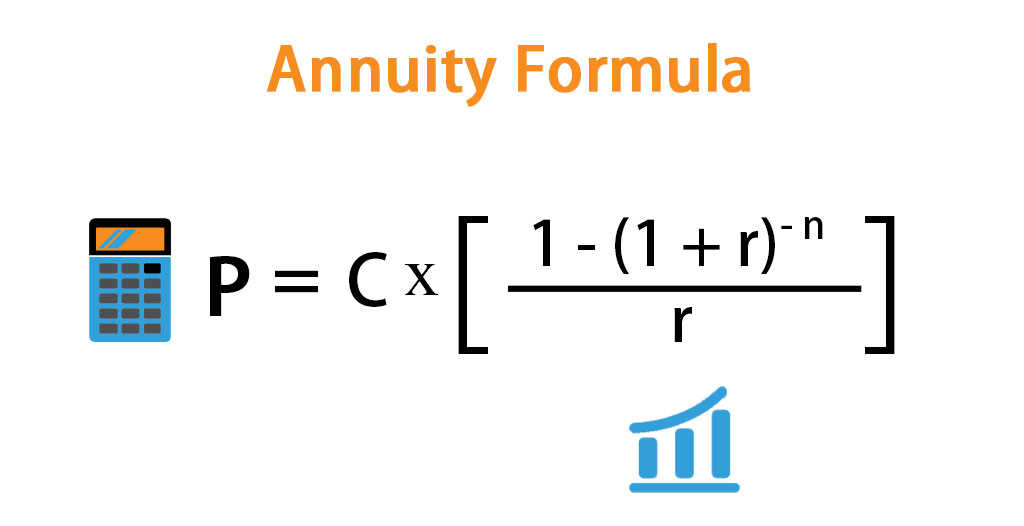

/CalculatingPresentandFutureValueofAnnuities1-0cea56f3b4514e44bed8f45d9c74011e.png)